Counting the prime numbers

Jon Maiga, 2021-08-19

In my last article I wrote about an estimation of the prime counting function, $\pi(n)$. This inspired me to try creating an exact function. Below I present a couple of impractical formulas I found experimentally. There is so much research in the area so I doubt anything below is original.

A recursive formula for the nth primorial

A primorial is like the factorial ($4!=1\cdot2\cdot3\cdot4=24$) but only prime numbers are used in the multiplication, e.g. $2\cdot3\cdot5\cdot7=210$. We will be using at the second definition of primorials A034386, where the value bumps at indices of primes, $p_n\#$:

1, 1, 2, 6, 6, 30, 30, 210, 210, 210, 210, 2310, 2310, 30030, 30030, 30030, 30030, 510510, 510510, 9699690, 9699690, 9699690,

I wanted to see if sequencedb could find some simple formulas for the nth primorial, $p_n\#$. For the automatic search the elementary +,-,*,/ together with the greatest common divisor $\gcd$ and a few other “elementary” functions. One of the simpler generated formulas is the following, with $p_0\#=1$

$$p_n\#=\gcd(n,\gcd(n, p_{n-1}\#)-1)\cdot p_{n-1}\#$$

Proof. Let’s examine the two cases, $n$ is composite or $n$ is prime.

If $n$ is composite, then the innermost $\gcd(n, p_{n-1}\#)$ equals the square free kernel of $n$, $rad(n)$. We then subtract one and again check the greatest common divisor with $n$, $\gcd(n, rad(n)-1)$ in a second step.

Since $\gcd(n,n-1)=1$ we get $\gcd(rad(n), rad(n)-1)=1$ which in turn implies that $\gcd(n,rad(n)-1)=1$ (since $n$ has the same prime factors as $rad(n)$). This means that if $n$ is composite we get $p_n\#=1\cdot p_{n-1}\#$.

When $n$ is a prime number, the innermost $\gcd(n, p_{n-1}\#)$ equals one since $n$ is not yet in the primorial. We then subtract one and again check the greatest common divisor with $n$, $\gcd(n, 1-1)=\gcd(n,0)=n$. This means that if $n$ is prime we get $p_n\#=n\cdot p_{n-1}\#$.
$\square$

It turns out that this double gcd structure can be used to create an indicator function for primes. Pretty neat!

primorial[0]=1;
primorial[n_]:=primorial[n]=GCD[n, GCD[n, primorial[n-1]]-1]*primorial[n-1]

Formulas for the prime counting function

From our recursive formula, $p_n\#$ we can describe the prime counting function, $\pi(n)$, the number of prime numbers less or equal to $n$ A000720

 0, 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 13, 13, 14, 14, 14, 14, 15,

$$\pi(n)=\sum_{k=2}^{n}(\gcd(k,\gcd(k, p_{k-1}\#)-1)-1)/(k-1)$$

You recognize the double $\gcd$ structure from our primorial definition, the extra subtraction and division just transforms it into the characteristic function of primes (1 if $n$ is prime else $0$). The final summation just adds ones and zeros up.

Note that as an optimization it’s enough to check the greatest common divisors of $k$ against the square root of $k$-th primorial (replace $p_{k-1}\#$ by $p_{\lfloor{\sqrt{k}\rfloor}}\#$).

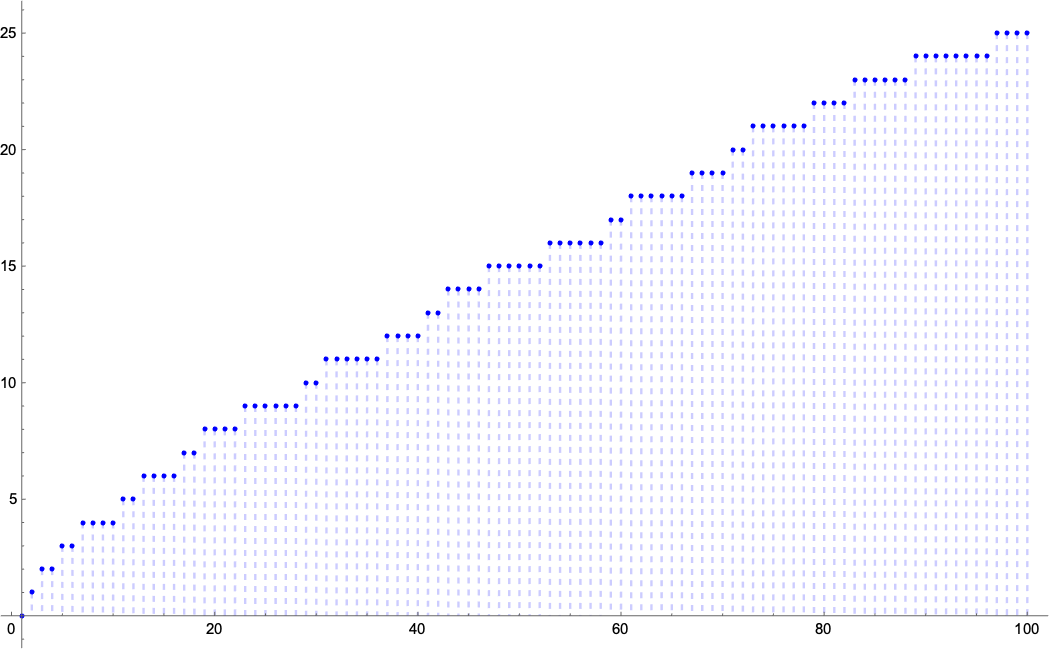
primorial[0]=1;
primorial[n_]:=primorial[n]=GCD[n, GCD[n, primorial[n-1]]-1]*primorial[n-1]
pi[n_]:=Sum[(GCD[k,GCD[k,primorial[k-1]]-1]-1)/(k-1),{k,2,n}]

With the factorial

Another version can be obtained by replacing the primorial by the factorial, again by utilizing the double gcd structure

$$\pi(n)=\sum_{k=2}^{n}(\gcd(k,\gcd(k, (k-1)!)-1)-1)/(k-1)$$

pi[n_] := Sum[(GCD[k, GCD[k, (k - 1)!] - 1] - 1)/(k - 1), {k, 2, n}]

In fact if we use the factorial we do not need the double $\gcd$ and can get away with something like (note that we need to start counting at $n=5$)

$$\pi(n)=2+\sum_{k=5}^{n}(k-\gcd(k, (k-1)!))/(k-1)$$

pi[1] = 0; pi[2] = 1; pi[3] = 2;
pi[n_] := 2 + Sum[(k - GCD[k, (k - 1)!])/(k - 1), {k, 5, n}]

Almost exact with using a step function

Instead of using our double $\gcd$ structure to create the indicator function for primes here we use a Heavyside step function

$$\pi(n)\approx\frac{1}{2}\left(n-1-\sum_{k=2}^{n}\tanh\left(s\cdot\gcd(k, (k-1)!) - \frac{3s}{2}\right)\right)$$

Where $s$ is any value greater or equal to $1$ and is used to sharpen then Heavyside function.

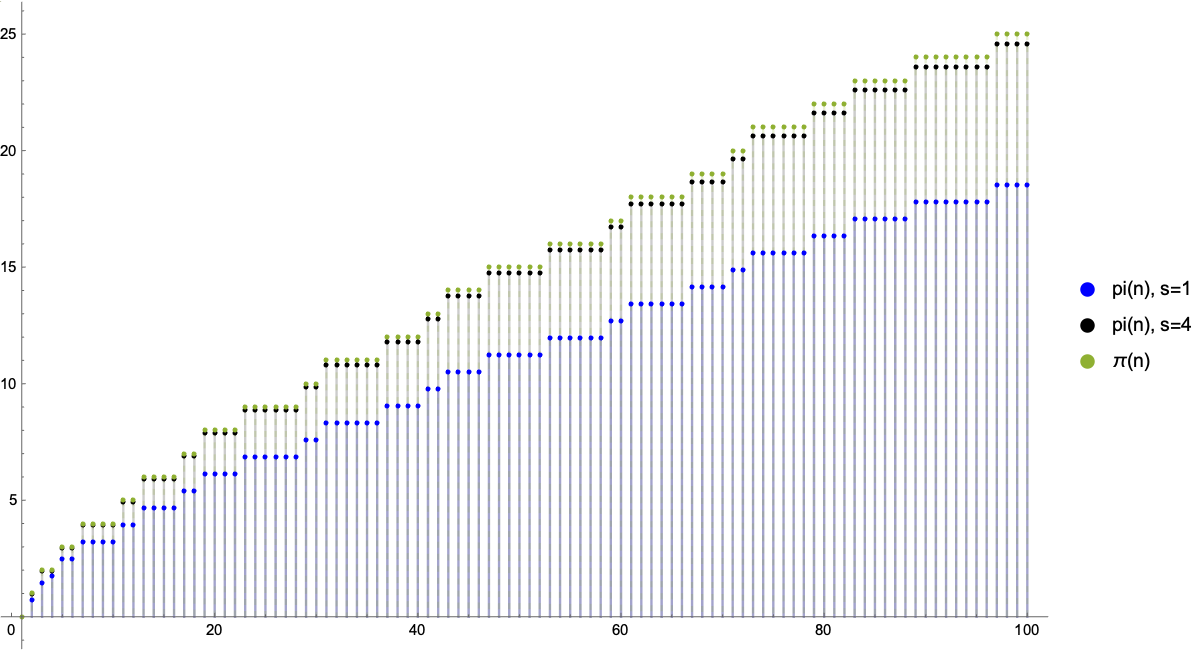
pi[n_,s_]:=1/2(n-1-Sum[Tanh[s*GCD[k,(k-1)!]-3s/2],{k,2,n}])

Almost exact with product of cosines

First note that $\frac{(n-1)!}{n}$ is an non-integer iff $n$ is prime, from this it’s we create the following function $\cos(\frac{k\pi(n-1)!}{n})$, where $k$ runs from $1$ to $n-1$.

If $n$ non prime each cosine will be $1$.

If $n$ is prime wil will get $n-1$ cosines in the between $-1$ and $1$ exclusive. A bit informally, the products of those tends towards 0 as $n$ goes on to larger and larger primes.

$$\pi(n)\approx n-\sum^{n}\prod_{k=1}^{n-1}\cos\left(\frac{k\pi(n-1)!}{n}\right)$$

We just sum the products up, invert the result (the leading $n-$) and there we have it, an accurate but inefficient prime counting function!

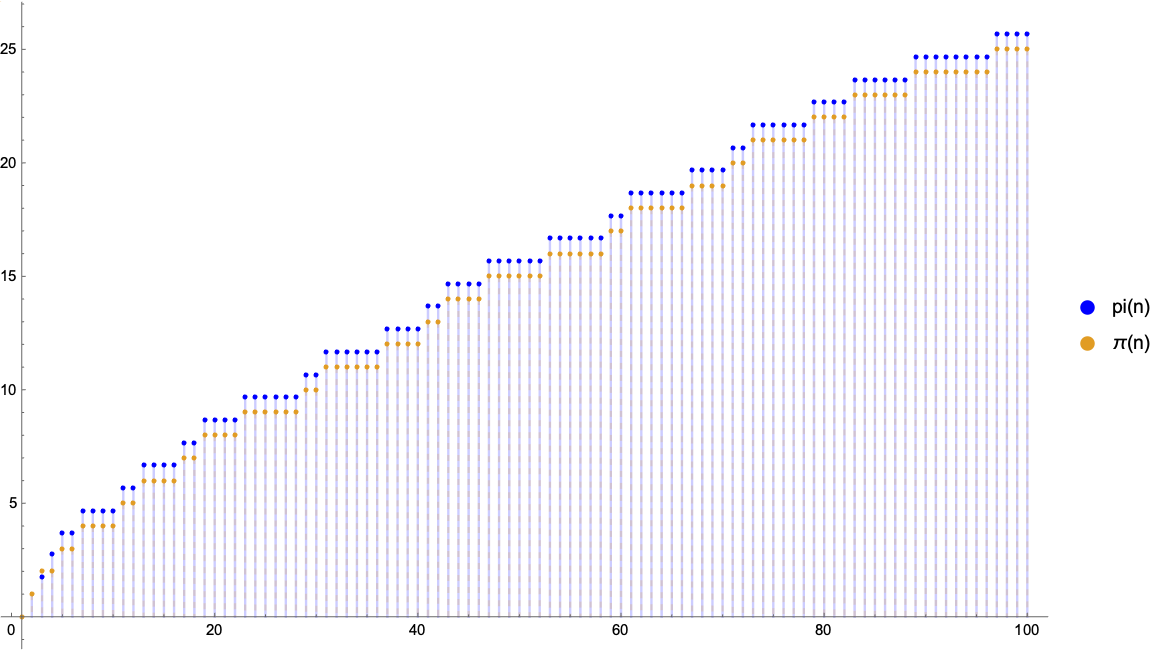
The slight offset can probably easily be fixed by e.g. exponentiating the product. But let’s keep it simple.

cp[n_]:=Product[Cos[k*(n-1)!*Pi/n],{k,n-1}]
pi[n_]:=n-Sum[cp[k],{k,n}]

Conclusion

None of the formulas above are practical but it was fun to tinker a bit. I wonder if any of those can be turned into something more analytical than discrete sums and products…