Improved mx3 and the RRC test

TLDR; I’ve updated mx3 with a slightly different construction that improves the quality a lot!

uint64_t mix(uint64_t x) {
	x ^= x >> 32;
	x *= 0xbea225f9eb34556d;
	x ^= x >> 29;
	x *= 0xbea225f9eb34556d;
	x ^= x >> 32;
	x *= 0xbea225f9eb34556d;
	x ^= x >> 29;    	
	return x;
}

The RRC mixer test

After my first investigation of mixers I was very lucky to get in contact with Pelle Evensen. He kindly pointed out a couple of mistakes in my articles (I’ve updated). He also introduced me to a test he had invented for mixers, RRC - Rotate, Reverse and Complement.

When I first created the old mx3 mixer I always had a nagging feeling that it probably isn’t sufficient to just benchmark it on the counting number, starting at zero and increasing by one for each mix operation that is sent to PractRand. The higher bits will never set (depending on how far PractRand goes before failing).

Pelles RRC-scheme gets around this by applying simple transforms on the counting numbers. The result is that the input to the mixer comes from all bits. So instead of just passing

mixer(counter++);

to PractRand one would do something like this

inline uint64_t rrc(uint64_t c, int rot, rrc_type type) {
	switch (type) {
	case rrc_type::identity: return ror64(c, rot);
	case rrc_type::reverse: return ror64(reverse64(c), rot);
	case rrc_type::complement: return ror64(~c, rot);
	case rrc_type::reverse_complement: return ror64(~reverse64(c), rot);
	}
	assert(false);
	return 0;
}

mixer(rrc(counter++, rot, type));    

where rot goes from 0 to 63 for all four types.

While there could be more/different transforms applied, RRC is a huge improvement over my previous testing methodology.

It’s with this scheme Pelle could verify his awesome nasam mixer that at least passes PractRand $2^{42}$. This means that non of the 256 PractRand runs fails before $2^{43}$ bytes. Yes it takes a lot of time to run those tests and it helps with a fast multicore computer!

In all tests I’ve used PractRand 0.94 with the flag -tf 2.

Below I’ve examined different constructions to see how far I could push them through with RRC testing.

Tuning xmxmx

This is the murmur3 and splitmix construction, unfortunately it fails the RRC test really early. Only looking on the worst case, I was able to find a configuration that “pushed” it to $2^{20}$ bytes in the worst case.

The multiplication constant is the one found here.

uint64_t xmxmx(uint64_t x) {
	x ^= x >> 32;
	x *= 0xe9846af9b1a615dull;
	x ^= x >> 32;
	x *= 0xe9846af9b1a615dull;
	x ^= x >> 28;    	
	return x;
}

I am afraid it’s not possible to get it significantly better, no matter which constants you choose. It’s certainly possible to find configurations with better balance between the four subsets, but I believe it will stay around $2^{20}$ for the worst case, which is our relevant metric.

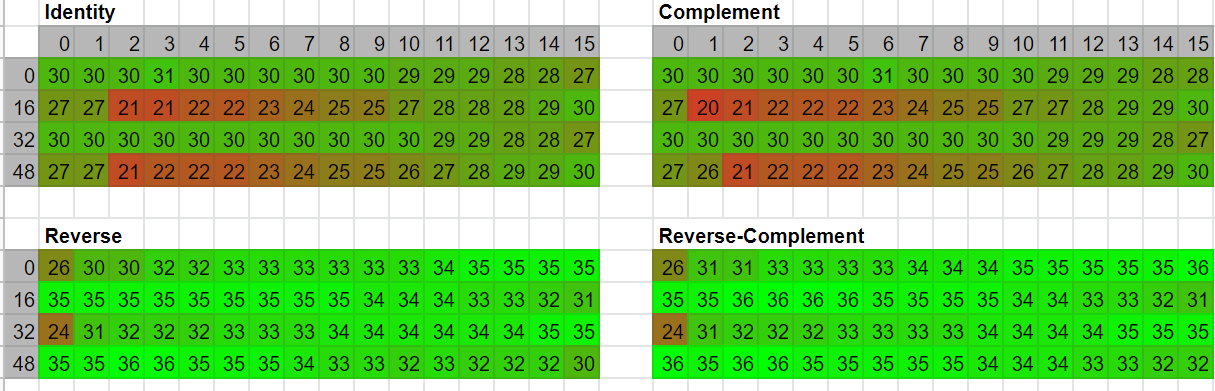
The image above displays all 256 xmxmx PractRand runs through RRC, the greener the further the test was able to run. I will not show more images of RRC but only report it’s worst case from here on.

As a note I quickly tried some variants with two multiplications for example xx-mx-mxx that took it to around $2^{31}$, for example

uint64_t xmxmx(uint64_t x) {
	x ^= (x >> 42) ^ (x >> 22);
	x *= 0xe9846af9b1a615dull;
	x ^= x >> 22;
	x *= 0xe9846af9b1a615dull;
	x ^= (x >> 42) ^ (x >> 22);
	return x;
}

Tuning mxmxmx

In my old mx3 mixer I used this configuration, this was before I was aware of the RRC test. Running my old configuration through it, showed really bad worst cases of $2^{21}$ in RRC. To remedy this I searched for new xor-shift constants.

To narrow down the search space, I first did an exhaustive search with two constants, like this mx-my-mx, this would create a matrix with worst cases. Then in the most promising clusters I ran a full search, a ‘cube’, mx-my-mz around those and selected the one with highest RRC worst case and the least fails

uint64_t mix(uint64_t x) {
    x *= 0xbea225f9eb34556d;
    x ^= x >> 41;
    x *= 0xbea225f9eb34556d;
    x ^= x >> 26;
    x *= 0xbea225f9eb34556d;
    x ^= x >> 42;
    return x;
}

With this configuration the worst case RRC become $2^{34}$.

I don’t think it’s possible to push it much further in terms of the RRC test.

While $2^{34}$ is way better than before, it has quite a bit to go to Pelle Evensens excellent nasam mixer that passes $2^{42}$.

The only way forward is to add more instructions!

Ad-hoc heuristics

With better mixers testing gets slow, so I needed to limit the search space somehow so instead of using a ‘good’ multiplier constant, I exchanged it with a crappy. A constant that would fail mixer much earlier than usual. The one I used was 6148914692327385771, it’s basically zeros and ones interleaved with some mutations, see this c_found here.

So instead of having to wait for a full RRC round mixers would fail earlier with the crappy multiplier, e.g
mx3 fails at $2^{15}$, mxmxxmx and most of its cousins fails at best around $2^{24}$ (probably overfitting in this case since I used the crappy in the search) and nasam which normally passes $2^{42}$ already fails at $2^{19}$.

Note that there is no guarantee that this is a good heuristic it’s just something I though could help. E.g. I’ve no evidence that a bad result from a crappy multiplier constant implies a bad result with a good. But there seems to be a tangible empirical relationship, good enough for my purposes!

Tuning mxmxxmx

Here things start to get decent, but also very slow to test. By using the ad hoc search heuristics I isolated a few candidates. I tested two of those candidates and both failed earliest on $2^{40}$ bytes.

uint64_t mix(uint64_t x) {
    x *= 0xbea225f9eb34556d;
    x ^= x >> 43;
    x *= 0xbea225f9eb34556d;
    x ^= (x >> 23) ^ (x >> 41);
    x *= 0xbea225f9eb34556d;
    x ^= x >> 28;
    return x;
}

The other candidate had xor constants 37-21-34-28.

I’m uncertain how much this can be improved by selecting different constants. I also tried mxx-mx-mx, mx-mx-mxx, mxx-mx-mxx even some short testing with mxx-mxx-mxx but none were outstanding with the crappy multiplier (heuristics) and in some limited full tests. I decided it was not worth the wattage to continue the search.

Passing 2^42 with xmxmxmx

Now with xmxmxmx it was clear that it was on a completely different level as it took the crappy constant to $2^{35}$ in RRC tests!

With this in hand I could look for a cluster of good xor constants like before. After finding a few such I basically took the candidate with constants closest to $32$ and started a full RRC test with a proper multiplier constant (the mx3 constant). After weeks of running the test the result came back and it had passed the $2^{42}$ (just like nasam!) without any notable problems (two early suspicious and a healthy dose of mildly suspicious and unusual remarks which is expected.)

uint64_t mix(uint64_t x) {
    x ^= x >> 32;    
    x *= 0xbea225f9eb34556d;
    x ^= x >> 29;
    x *= 0xbea225f9eb34556d;
    x ^= x >> 32;
    x *= 0xbea225f9eb34556d;
    x ^= x >> 29;
    return x;
}

Not that it has the same number of xor constants as mxmxxmx but one x has been moved to the front.

mx3 revision 2

Since I suspect that mx3 is pretty unused so far I’ve decided to bluntly update it with the newly found constants and the initial xor-shift and keep the name (I could have renamed it to x-mx3 but let’s keep it simple).

I have also optimized the stream mixer in the mx3 hasher with RRC to find better xor-constants as well.

The second revision of mx3 is slightly slower, but the quality gain is enormous.

mixer	MSVC, Threadripper 3970x@3.7GHz, ms	MSVC, i7-4790k@4GHz, ms	Clang, i7@2GHz (mac), ms	RRC
nop	1133	1148	1300	-
splitmix	4047	4716	7917	16
mx3 old	4213	4688	7557	21
mx3 new	5173	5975	10335	>42

In this speed test I simply pushed a counter through the mixers, however I encourage you to verify the result.

Final thoughts

This project, which was supposed to take two weeks has now spanned over months, mostly because testing takes a lot of CPU hours.

Finally I really want to thank Pelle for explaining a lot of details with mixers, introducing me to the RRC test and for telling a lot of fun anecdotes - I really recommend you go and read his blog.