Approximating the prime counting function

Jon Maiga, 2021-08-08

In the end of 18th century Gauss guessed that there where about $\frac{x}{log(x)}$ primes up to $x$. This was later proved as the prime number theorem together with the more accurate logarithmic integral, $li(x)$ as an approximation.

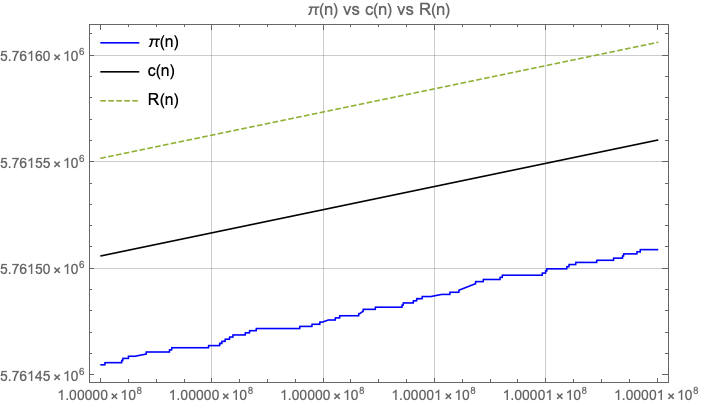
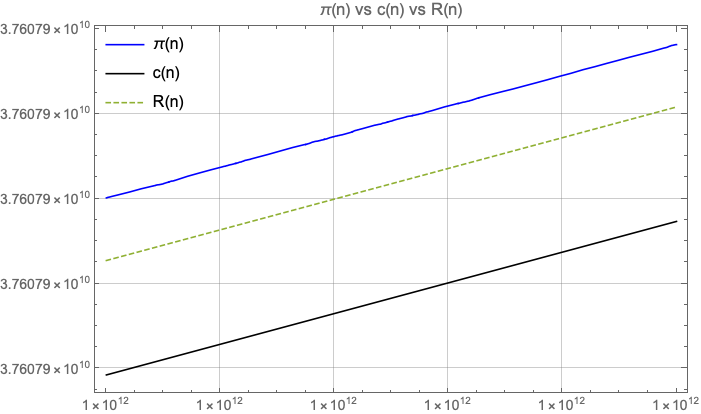
Here we show a similar estimation based on an observation of the number of primes less than a square. From that we create a continuous function to approximate the prime counting function $\pi(x)$. The approximation appears to yield similar results to the Riemann prime counting function, $R(x)$.

An observation of the number of primes up to a square

While playing with sequencedb.net it was observed that the simple recurrence

$$a(n)=\frac{n-1}{\log(n)} + a(n-1)$$

seems to yield a good estimate of the number of primes between $0$ and $n^2$.

$n$	$a(n)$	$\pi(n^2)$	$a(n)-\pi(n^2)$	$li(n^2)-\pi(n^2)$
10	25	25	0	5
100	1226	1229	-3	17
1000	78521	78498	23	130
10000	5761505	5761455	50	754
100000	455050326	455052511	-2185	3104
1000000	37607907843	37607912018	-4175	38263

If we expand the recurrence $a(n)$ for $n>1$ it looks like this

$$a(n)=\frac{1}{\log(2)}+\frac{2}{\log(3)}+\cdots+\frac{n-1}{\log(n)}$$

So it seems like $\frac{n-1}{\log(n)}$ approximates the number of primes between the two consecutive squares $(n-1)^2$ and $n^2$

$$\frac{n-1}{\log(n)} \approx \pi(n^2)-\pi((n-1)^2)$$

Comparison with the PNT

The $a(n)$ approximation is close to what we get from the prime number theorem $li(n^2) \approx \sum_{k=1}^{n}\frac{d}{dk}li(k^2) = \sum_{k=1}^{n}\frac{k}{log(k)}$, this gives $li(n^2)-li((n-1)^2) \approx \frac{n}{log(n)} \approx \pi(n^2)-\pi((n-1)^2)$.

While Gauss correctly guessed (apparently at the age of 15!) that there are about $\frac{n}{log(n)}$ primes up to $n$, the version with the logarithmic integral improves this guess by saying, there are about $\frac{n}{log(n)}$ between two consecutive squares.

The observed formula $a(n)$ states that there are about $\frac{n-1}{log(n)}$ between two consecutive squares, so it’s a bit more conservative than the $li$ version.

Making our approximation work for all x

We can express the recurrence, $a(n)$ as the sum

$$a(n)=\sum_{k=2}^{n}\frac{k-1}{\log(k)} \approx \pi(n^2)$$

This discrete sum estimates the number of primes less than a given square. But what if we want to approximate something that is not a perfect square like $a(30)$? Calculus to the rescue! Let’s replace the sum by an continuous function by taking the integral

$$\int \frac{x-1}{\log(x)}dx=li(x^2)-li(x) + C$$

where $li$ is the logarithmic integral. We set $c=0$ and we also adjust the offset so we get

$$\pi(x^2)\approx b(x)=li((x+\frac{1}{2})^2)-li(x+\frac{1}{2})$$

Sure enough, giving it a test drive yields results very close to $a(n) \approx b(n)$.

With our continuous prime counting function $b(x)$ we should now be able to approximate the number of primes for any number. To do that, we just take the square root of $x$ and pass it in to $b$. Let’s create a new function that counts the primes up to $n$ instead of $n^2$, that is $c(n)=b(\sqrt{n})$. I also expanded the argument to the first $li$

$$\pi(n) \approx c(n)=li(n+\sqrt{n}+\frac{1}{4})-li(\sqrt{n}+\frac{1}{2})$$

Voilà - we have a prime counting function! Some tests show promising results (see table later for more results and comparisons)

$c(10)=4.84 \approx \pi(10)=4$
$c(100)=25.95 \approx \pi(100)=25$
$c(1000)=168.57 \approx \pi(1000)=168$
$c(10000)=1227.78 \approx \pi(10000)=1229$
$c(100000)=9586.04 \approx \pi(100000)=9592$
$c(1000000)=78522.3 \approx \pi(1000000)=78498$

Riemann prime counting function

We already mentioned that $\pi(n) \approx li(n)$ so we will use that in our comparisons. Further, we add another well known approximation, namely the Riemann prime counting formula

$$R(x)=\sum_{n-1}^{\infin} \frac{\mu(n)}{n}li(x^{1/n})$$

where $\mu$ is the Möbius function. One interesting thing is that $c(n)$ seems to be stay pretty close to $R(n)$.

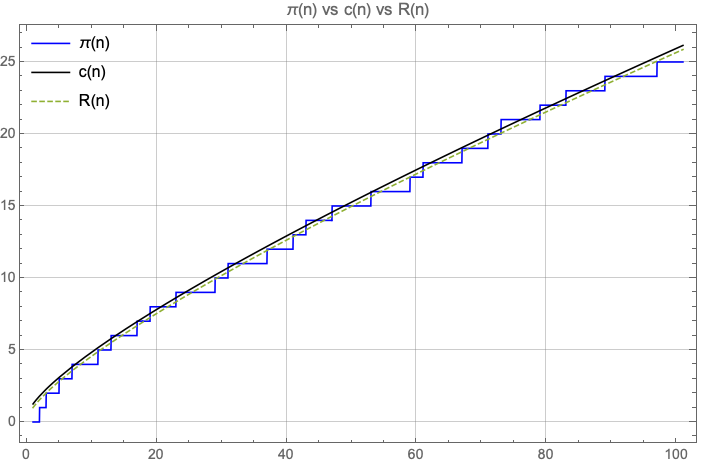
See tables below for a comparison between $c(n)$, $li(n)$ and $R(n)$.

Conclusion

My gut feeling is that $c(x)$ is slightly behind $R(x)$ in terms of accuracy (at least for $n<10^{12}$), but at the same time $c(x)$ seems simpler. While $R(x)$ uses the Möbius function and the logarithmic integral, $c(x)$ only uses the logarithmic integral.

Mathematica

a[n_Integer]:=Sum[(k-1)/Log[k], {k,2,n}]
b[x_]:=LogIntegral[(x+1/2)^2]-LogIntegral[x+1/2]
c[x_]:=LogIntegral[x+Sqrt@x+1/4]-LogIntegral[Sqrt@x+1/2]

Tables

In all the comparison tables below the values are rounded to the nearest integer.

Power of ten

The mathematica version of $\pi$ only works to about $10^{14}$, so for this table I resorted to the great Online Encyclopedia of Integer Sequences, entry A006880 - “the number of primes < 10^n”.

$k, n=10^k$	$c(n)-\pi(n)$	$R(n)-\pi(n)$	$li(n)-\pi(n)$
1	1	1	2
2	1	1	5
3	1	0	10
4	-2	-2	17
5	-6	-5	38
6	24	29	130
7	73	88	339
8	51	97	754
9	-207	-79	1701
10	-2183	-1828	3104
11	-3298	-2318	11588
12	-4174	-1476	38263
13	-13218	-5773	108971
14	-39818	-19200	314890
15	15868	73218	1052619
16	166763	327052	3214632
17	-1048475	-598255	7956589
18	-4772209	-3501366	21949555
19	20279712	23884333	99877775
20	-15163730	-4891825	222744644
21	-115833916	-86432204	597394254
22	-211645366	-127132665	1932355208
23	789410232	1033299853	7250186216
24	-2365439590	-1658989719	17146907278
25	-3888233187	-1834784714	55160980939
26	-23137628496	-17149335456	155891678121
27	-35051971558	-17535487934	508666658006
28	-226144684235	-174760519827	1427745660374

Power of two

$n$	$c(n)-\pi(n)$	$R(n)-\pi(n)$	$li(n)-\pi(n)$
2	1	1	0
4	1	0	1
8	0	0	1
16	1	0	3
32	0	0	3
64	0	0	4
128	0	0	5
256	1	0	7
512	-1	-1	7
1024	0	0	9
2048	1	1	12
4096	-1	-1	13
8192	2	2	20
16384	-3	-3	20
32768	3	4	32
65536	4	6	42
131072	-3	-2	45
262144	6	9	69
524288	-18	-14	64
1048576	5	11	113
2097152	-12	-5	129
4194304	-20	-10	167
8388608	0	15	249
16777216	20	40	351
33554432	-147	-119	296
67108864	-53	-14	541
134217728	32	85	830
268435456	-141	-70	935
536870912	102	199	1555
1073741824	-521	-388	1448
2147483648	-5	175	2666
4294967296	232	477	3861
8589934592	-1354	-1021	3586
17179869184	-1399	-948	5335
34359738368	1471	2084	10664
68719476736	980	1811	13544
137438953472	-1196	-70	15995
274877906944	-718	810	22831
549755813888	-6550	-4477	25740
1099511627776	-2673	140	41645

Sequences

The 100 first terms are rounded to the nearest integer below

a(n)

0,1,3,5,8,11,14,17,21,25,29,33,38,43,48,53,59,65,71,77,84,91,98,105,113,120,128,136,145,153,162,171,180,189,199,209,219,229,239,250,260,271,283,294,305,317,329,341,354,366,379,392,405,418,432,445,459,473,487,502,516,531,546,561,577,592,608,624,640,656,672,689,706,723,740,757,775,792,810,828,847,865,883,902,921,940,959,979,998,1018,1038,1058,1079,1099,1120,1141,1162,1183,1204,1226

b(n)

1,3,5,7,9,12,15,18,22,26,30,35,39,44,49,55,60,66,72,79,85,92,99,106,114,121,129,137,146,154,163,172,181,190,200,210,220,230,240,251,262,273,284,295,307,318,330,343,355,367,380,393,406,419,433,447,460,474,489,503,518,532,547,563,578,593,609,625,641,657,674,690,707,724,741,759,776,794,812,830,848,866,885,903,922,941,961,980,1000,1020,1039,1060,1080,1100,1121,1142,1163,1184,1205,1227

c(n)

1,2,2,3,3,3,4,4,5,5,5,5,6,6,6,7,7,7,8,8,8,8,9,9,9,9,10,10,10,10,11,11,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,15,15,16,16,16,16,17,17,17,17,18,18,18,18,18,19,19,19,19,19,20,20,20,20,21,21,21,21,21,22,22,22,22,22,23,23,23,23,23,24,24,24,24,25,25,25,25,25,26,26,26

Yes I know, the function names are very creative.