A few good looking recursive functions

Jon Maiga, 2019-06-11

Every now and then I run into functions that makes me go “wow this looks different”!

In this post I will list a few simple recursive formulas that yield somewhat surprising graphs. I will settle with noting they look nice and leave further analysis to the reader.

1 - the braid

Let’s start with a simple

$a(n)=\frac{n-a(n-1)}{a(n-2)} \tag{1}$

With the initial values of $a(0)=a(1)=1$ we get

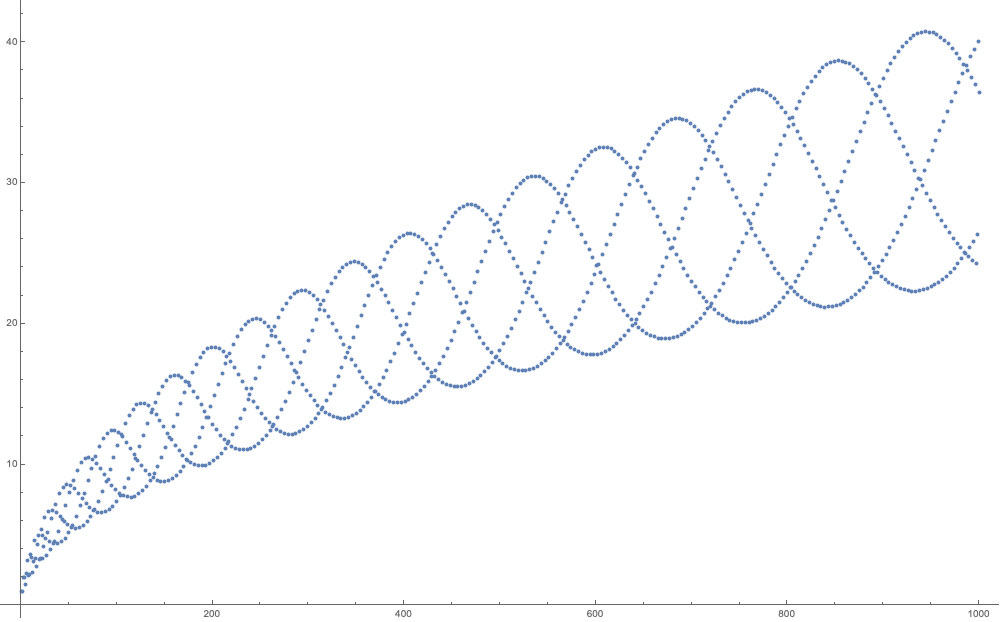
The simple recursive function (1) creates a braid that seems to follow $\sqrt n$. What are the upper and lower bounds?

Now if we take the first differences of (1) $(a(n)-a(n-1))$ we get it centered around the x-axis

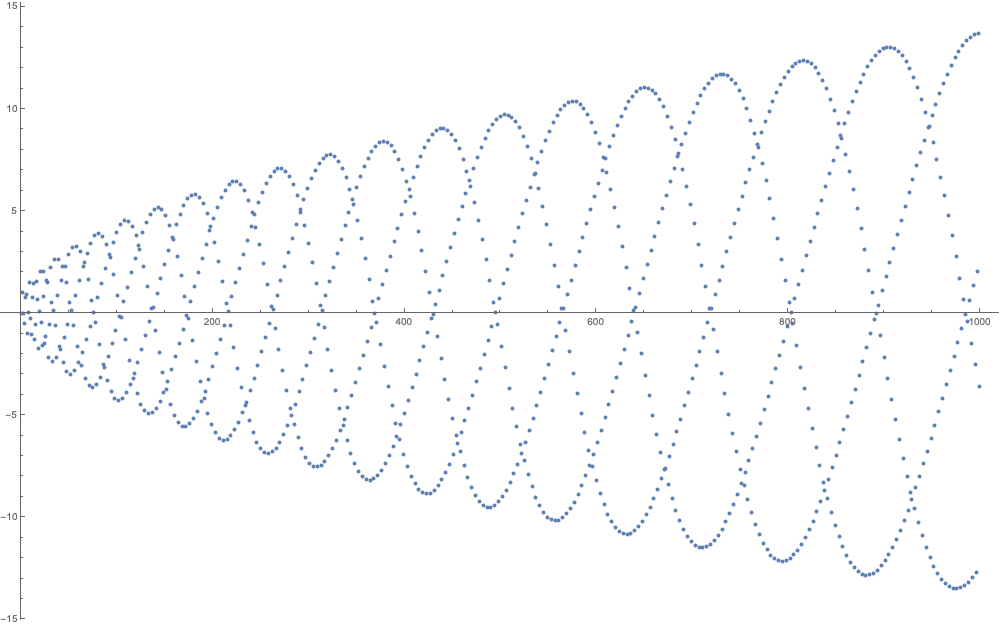
• What are the upper/lower bounds?
• What is the period? (if you can call it that)

2 - the weirdo

Changing the initial values of (1) dramatically changes the function, for example

$a(0)=1, a(1)=3$ gives us

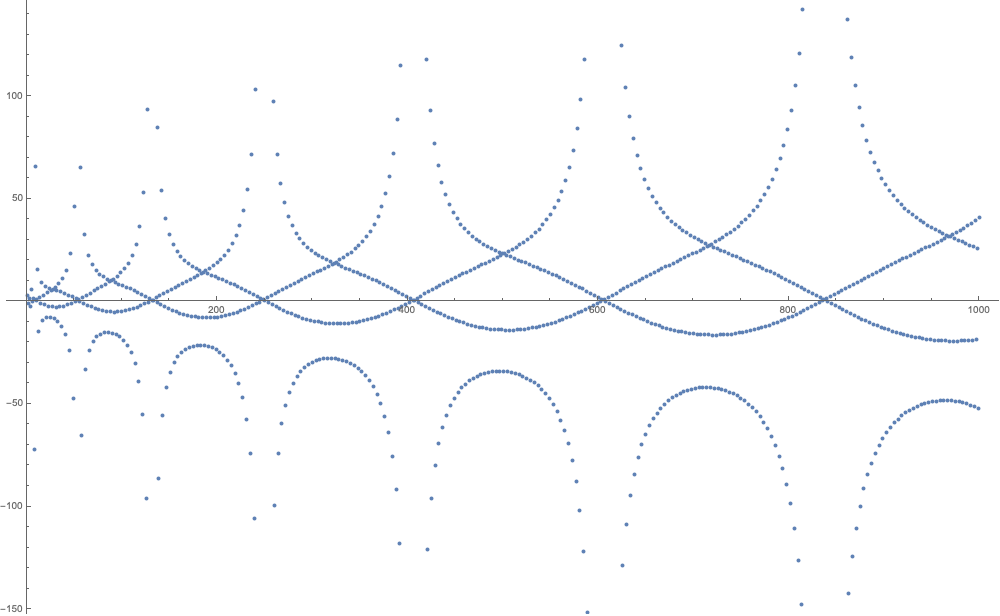
Note that this graph has some extreme values that have been omitted. Taking the first differences gives us

• Is there anything interesting going on where it seems to cross the x-axis?

3 - the Enterprise

Another remarkable plot is

$a(n)=-\frac{n}{a(n-2)}-a(n-1)$

With $a(0)=1$ and $a(1)=3$ we get

• Is there anything interesting about this one?

4 - ten curves in one

Another noteworthy is

$a(n)=a(n-1)^{a(n-3)-a(n-2)}+1$

With $a(0)=a(1)=a(2)=1$ we get

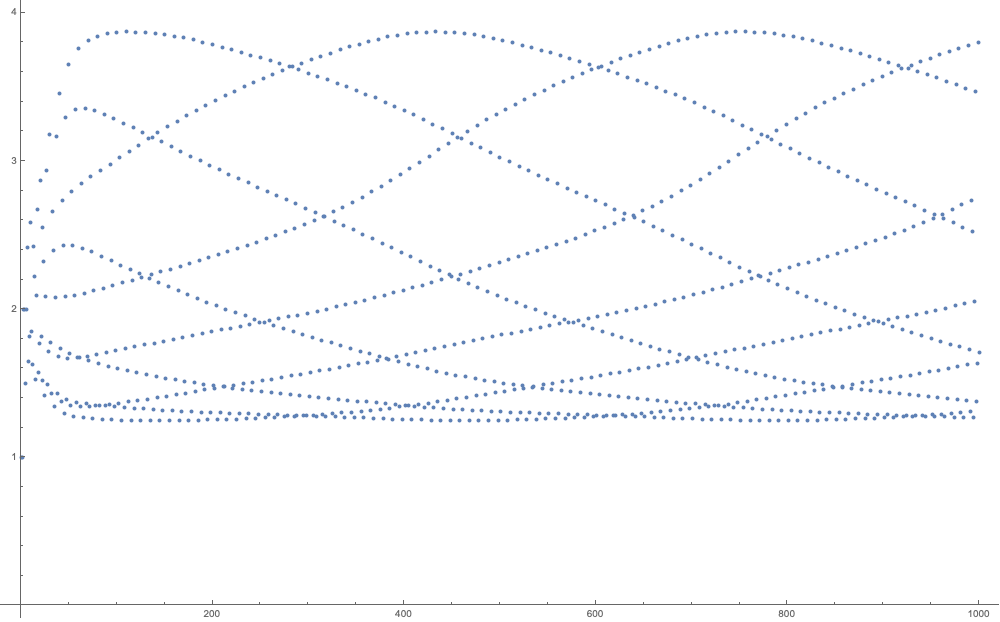
• Why is it split into ten different curves?

5 - heaps of primes

Finally, let’s look at one involving the primes

$a(n)=-\frac{p(n)}{a(n-1)}-a(n-2)$

With $a(0)=3$ and $a(1)=1$ we have

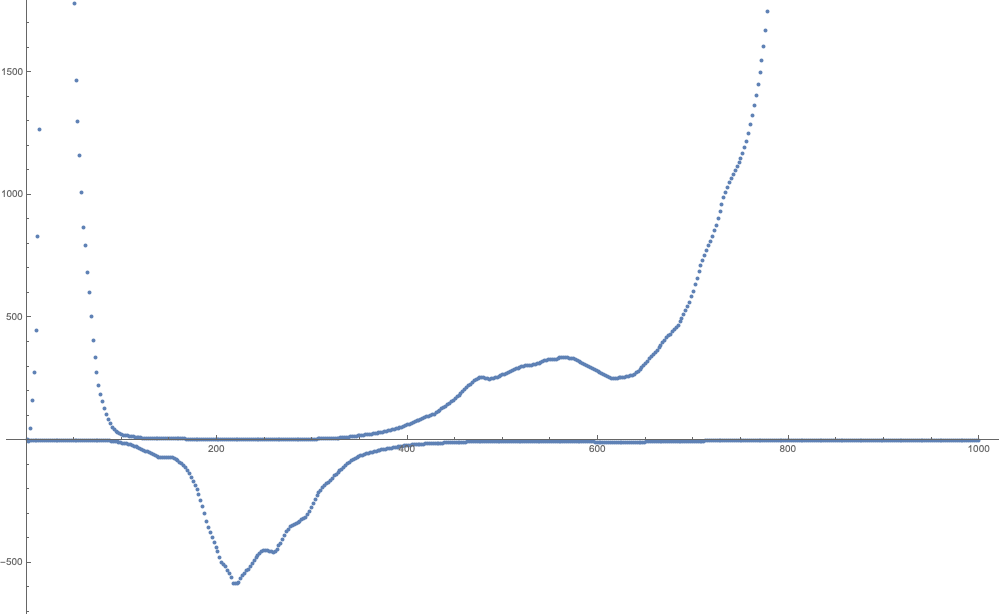
• What is this?

Conclusion

My gut feeling is that those are more the kind of function you look at than get anything sensible out of. Although I would be grateful for any feedback on those. I don’t even know (and haven’t looked much) if they have been studied?

All sequences was found while I was browsing sequencedb.net, a machine generated database with decimal and integer sequences.

Written with StackEdit.