Fun with signed nested exponentials and the prime numbers

Jon Maiga, 2018-07-31

While I was playing around with a hobby project, sequencedb.net, I encountered the recursive function
$a(n)=log(|(a(n-1)|)$

It caught my attention because of its random appearance and simplicity.

In this article I will display how to generate interesting integer sequences by carefully selecting a unique initial $a(0)$ value. Then I show how to find the initial value that generate prime numbers ($a_p(0)\approx-0.02172268$). Next I examine the number segmentation that takes place when reconstructing the prime sequence from $a_p(0)$. Finally I draw some conclusions and leave a bunch of questions.

As a computers scientist expect this to be pretty experimental. Here is a link to the function in the plot above.

Edit 2018-08-24: I submitted $a_p(0)$ to OEIS and it was approved today as A317547.

Overview

During the recursion of $a(n)=log(|a(n-1)|)$ the logarithm will eventually become negative. The next iteration flips it to the positive side and takes the log and the process continues, building nested logs on the form $a(n)=log(|log(|log(|log(|...|))))$

I was curious to find out what makes it irregular and what controls the gap between the positive $a(n)$ values.

Notice that, the closer a value lands to $\approx-0.56$, the longer it takes until the next spike (positive value). In the example above, around $n=30$, $a(n)$ lands closer to $-\Omega$ so the next spike is delayed until $n=44$.

This is because -0.56 is close to the solution to $log(x)=-x$. Solving x will give us the exact value $x=LambertW(1)=\Omega=0.5671...$

Apparently, the constant Lambert W(1) is called $\Omega$ (omega), so I’ll use it from here.

In fact, if the value lands exactly on $\Omega$ it would not produce any more spikes since $\Omega$ is the solution to $log(x)=-x$.

Associated integer sequences

The $n$ that spikes such that $a(n) > 0$ form a sequence of integers. For example, $a(0)=3$ => [0,1,2,4,7,12,16,19,…]

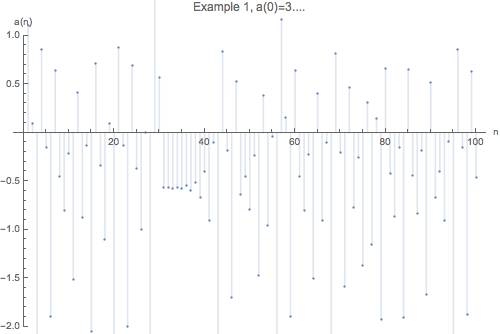
The initial value, $a(0)$, of the recursive function is our only control variable, in the particular example above $a(0)=3$, we get different sequences by changing this value , e.g. setting $a(0)=2$ generates spikes at [0,1,4,6,7,13,15,16,…]. You can compare the two $a(n)$ below.

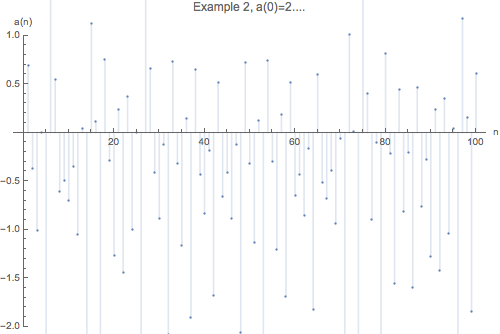
Those two sequences are probably not interesting, however we can generate interesting sequences by carefully selecting the initial value, $a(0)$.

Calculating a(0) for a sequence

To calculate $a(0)$ for sequence we need to find the inverse to $a(n)$. The inverse of the logarithm is the exponential, $log(e^x)=x$. Since we have nested logarithms, we need to nest exponentials for the inverse, e.g $log(log(log(e^{e^{e^x}})))=x$

What we want to find is nested exponentials that generate spikes for a given sequence of integers.

For example, to generate the odd numbers [1,3,5,7,9,11,13…] we start by creating a nested exponential, for as many odd numbers we want to generate, lets test with 4: $e^{e^{e^{e}}}$. Now before we calculate $a(n)$ with $a_o(0)$ we need to make sure it’s only positive for every odd term. To ensure this we negate the nth-even exponentials.

The pattern of signs will be [-,+,-,+…+,-], here are approximations with 5 and 9 term estimation

$a_o(0)\approx -e^{e^{-e^{e}}}\approx-1.4100451141548884$
$a_o(0)\approx -e^{e^{-e^{e^{-e^{e^{-e^{e^{-e}}}}}}}} \approx-1.3218185310130995$

We could continue the nesting to get closer to the actual limit, however since this pattern is repetitive we can solve the equation directly, by just looking at one period of the signs
$-e^{e^{-x}}=x$
Which gives $a_o(0)=x\approx-1.309799585804150...$

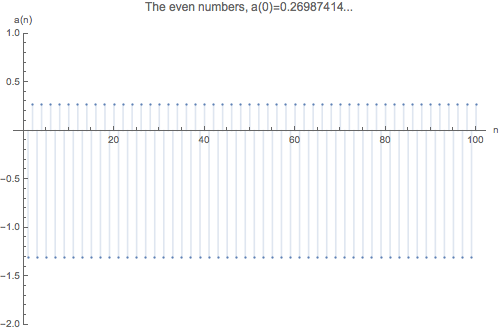
Similarly to calculate $a_e(0)$ for the even numbers [0,2,4,6,8,10,12,14…] we do the same but we shift the signs by one [+,-,+,-…-,+].
$a_e(0)=e^{-e^{x}}=x=0.269874137573449...$

For every periodic sequence, we can solve the equation to get an exact value of $a(0)$. Now, calculating $a(n)$ with $a_o(0)$ will produce the odd numbers and with $a_e(0)$ the even, until we run out of precision.

Links to recursive versions of $a_e(0)$ and $a_o(0)$ in sequencedb.net.

Signed nested exponentials

The general idea is to set the sign on the nth exponential to negative if we don’t want $n$ in the generated sequence. The equation $a(0)$ for any generable* sequence is to create signed nested exponentials, $(sne)$ according to:

$sne(n)=sf(n)e^{sne(n-1)}$

where $sf(n)$ is the sign function
$sf(n) = \begin{cases} 1, & \text{if $n \in$ sequence} \\ -1, & \text{if $n \notin$ sequence} \end{cases}$
then
$a(0)=\lim \limits_{n \to \infty}sne(n)$

The value of $sne(0)$ corresponds to the last generated integer, we can set it to an arbitrary value, say $0$, then $a(n)$ will land on $sf(n)e^0=\pm1$ in the final step.

Experimentally, it seems like every generable sequence has a unique constant, $a(0)$, associated with it. The uniqueness can probably be explained by the flipping the signs in the exponential tower. The analogue would be the bits in binary numbers.

*Limitations: Note that this process will blow up if the sequence isn’t sparse enough (too many consecutive 1’s), the negative sign makes it go towards $-\Omega$ while the positive sign quickly towards infinity. Also it requires monotonic sequences. With some modifications I think we could overcome those limitations, but that is for another occasion - and vacation.

The prime numbers emerge from a(0)=-0.021722689835612…

Now lets try to do the same for the prime sequence [2,3,5,7,11,13,17…]. Our sign function for primes is

$sf(n) = \begin{cases} 1, & \text{if $n$ is prime} \\ -1, & \text{if $n$ is composite} \end{cases}$

We calculate $sne_p(n)$, for as may primes as we want to encode into $a_p(0)$, we can see the convergence towards $a_p(0)$ here:

$n$	$sne_p(i)$
1	-0.367879441171442321595523770161
16	-0.0217082823745251626563514079137
31	-0.0217227023854698016559258754118
46	-0.0217226898321347349310824800486
61	-0.0217226898356109072110209881644
76	-0.0217226898356120841442223463747
91	-0.0217226898356120842741933187034
106	-0.0217226898356120842743019406735

Then we recursively calculate $a(n)=log(|(a(n-1)|) \quad a_p(0)=-0.021722689835612084274301...$ The plot looks like this

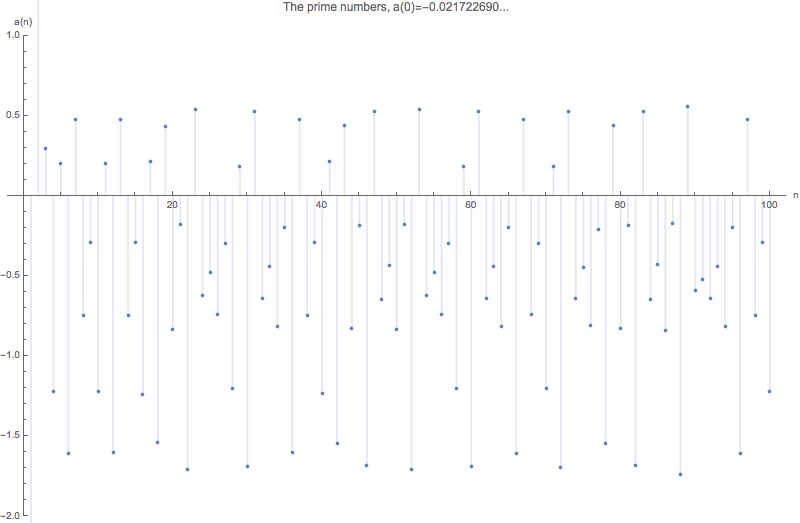
All the $n$ where $a(n)>0$ n the graph above are the prime numbers.

Voilà, we encoded the prime sequence into $a_p(0)$ and the we decoded it with the inverse. What is the point you may ask? Well, I am not sure :)

Edit 2018-08-24: The constant is now available in OEIS as A317547.

Segmentation of the primes

A side effect of unwrapping $a_p(0)$ is that we get some hierarchical number segmentation where each segment stretches out along the x-axis (the horizontal lines in the plot below). The dots represent the $a(n)$ values. It looks like a note paper and it makes me wonder how it would sound if played.

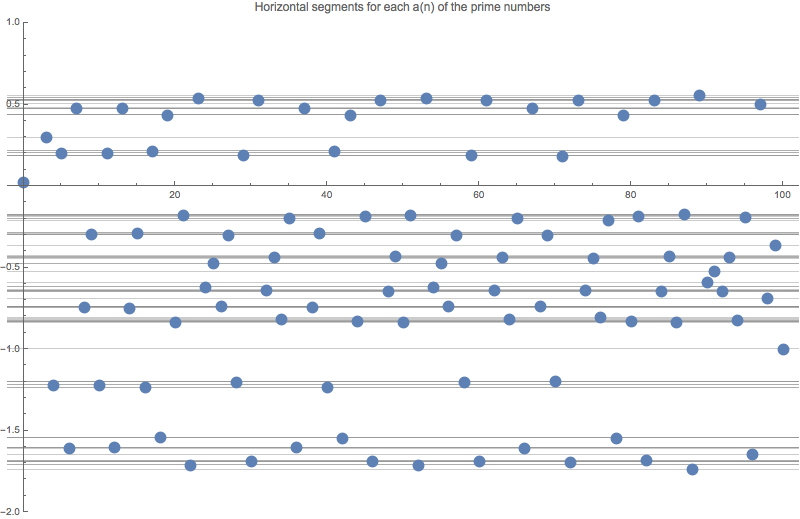
Since the primes are infinite we get infinite number of segments as well, one per each added $n$ (we can never land on exactly the same y-value more than once since we would get repetition then).

Now, if we add some arbitrary height to a segment we can find similar numbers, I’ve manually grouped a few of them to see what patterns arise.

The full graph represent all non negative integers (S0).

For $a(n)>0$ we find all the prime numbers (S1) and below the composites (S2), the prime numbers are roughly split into the lesser twin pairs (S4) and those with larger gaps (S3).

There is also a splitting on even and odd numbers, all odd numbers are above $-\Omega$ and the even under.

This segmentation continues, and numbers in the same segment have some similarity, mainly based on distance to other primes (or whatever the encoded sequence is). The reason is that each $a(n)$ needs to position itself to conform to the rest of the sequence. For example, all the lesser twin primes (S4), need to emit a positive spike in 2 steps so they all end up close to each other.

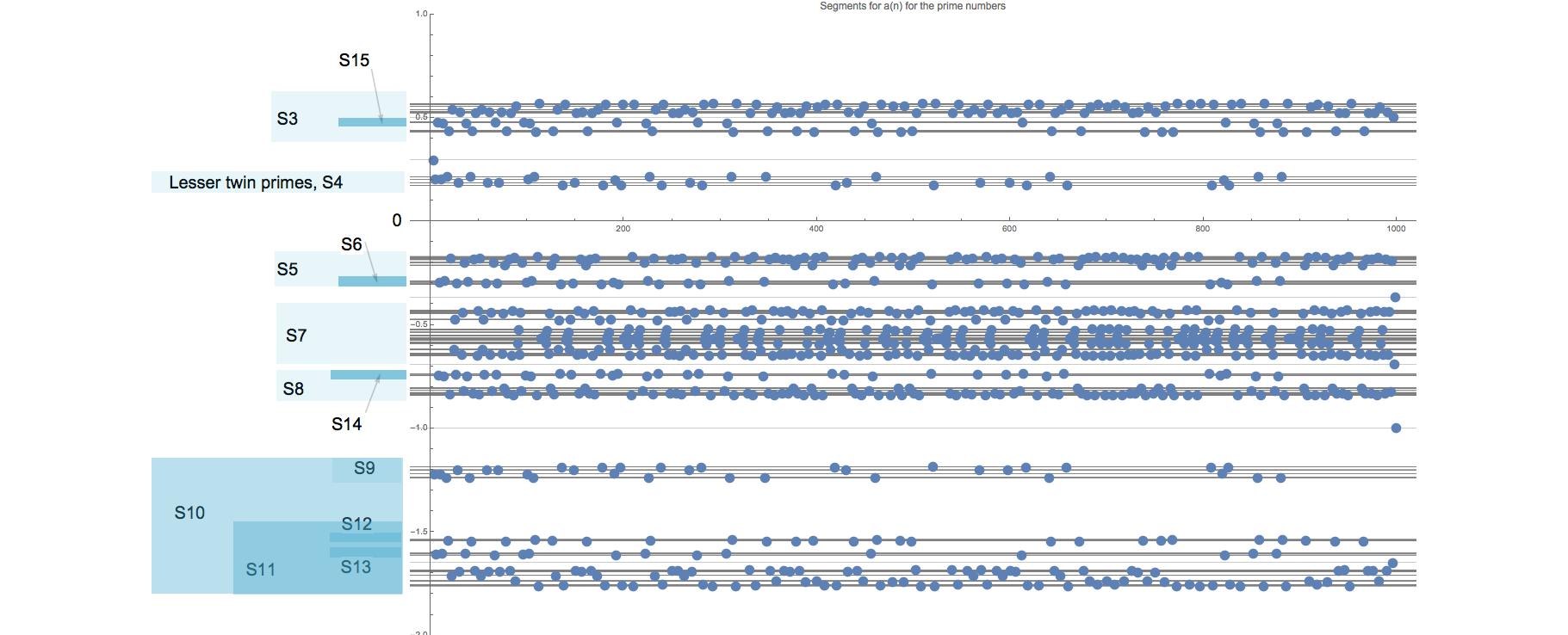
Although I left out S0, S1 and S2 in the plot above to make it more readable, it’s still not very easy to locate segments, graphics is not my strong side.

Below I’ve composed a very unorganised and incomplete list with some of the segments. I was able to look up some sequences in oeis.org, I also included some unrecognised sequences.

Segment	Oeis	Description	Sequence
S0	A000027	The natural numbers (all)	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,…
S1	A000040	The prime numbers ($a(n)>0$)	2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,…
S2	A002808	The composites ($a(n)<0$)	4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24,…
S3	A067774	Primes p so p+2 is not a prime.	(2,) 7, 13, 19, 23, 31, 37, 43, 47, 53, 61, 67, 73, 79,…
S4	A001359	Primes p so p+2 is a prime. Lesser twin primes.	(3,) 5, 11, 17, 29, 41, 59, 71, 101, 107, 137, 149, 179, 191,…
S5			21, 35, 45, 51, 65, 77, 81, 87, 95, 111, 125, 129, 155, 161,…
S6	A256388?	Composites n so n+2 is a lesser twin prime.	(1, 3,) 9, 15, 27, 39, 57, 69, 99, 105, 135, 147, 177, 189, 195, 225,…
S7			24, 25, 32, 33, 48, 49, 54, 55, 62, 63, 74, 75, 84, 85,…
S8			8, 14, 20, 26, 34, 38, 44, 50, 56, 64, 68, 76, 80, 86,…
S9	A144834	Numbers n+1 and n+3 are both prime.	4, 10, 16, 28, 40, 58, 70, 100, 106, 136, 148, 178, 190, 196,…
S10	A006093	a(n) = prime(n) - 1.	4, 6, 10, 12, 16, 18, 22, 28, 30, 36, 40, 42, 46, 52,…
S11	A141515	a(n) = phi(A067774(n)) where phi is Euler totient function.	6, 12, 18, 22, 30, 36, 42, 46, 52, 60, 66, 72, 78, 82,…
S12			18, 42, 78, 108, 126, 162, 228, 312, 348, 378, 396, 438, 462,… (GCD=6)
S13	A215918	Numbers n such that 6n + {1, 5, 7} are all primes. (S13/6)	6, 12, 36, 66, 96, 102, 192, 222, 276, 306, 456, 612, 822, 852, 876,…
S14	A243811	Numbers n such that 2n+3 and 2n+5 are both prime. (S14/2)	8, 14, 26, 38, 56, 68, 98, 104, 134, 146, 176, 188, 194, 224,…
S15	A022005	Initial members of prime triples (p, p+4, p+6)	7, 13, 37, 67, 97, 103, 193, 223, 277, 307, 457, 613, 823, 853,…

The list could go on, and it can be created with much more rigour.

I noted that this grouping in segments doesn’t seem to happen for arbitrary $a(0)$ such as the first 2 examples with $a(0)=2$ and $a(0)=3$, so maybe segments could be used to determine randomness of sequences. If segmentation occur, especially away from $-\Omega$ the sequence has a non random pattern.

There is also a clear symmetry around $-\Omega$, each segment has a corresponding segment on the opposite side S2-S10, S4-S9, S6-S8, S3-S11 and so on. Maybe I will look into this into the future.

You can also observe the segments for the first 1000 $a_p(n)$ in the appendix histogram.

Properties

Here are, what I think are some properties of $a(n)$.

1. Each generable sequence has a unique $a(0)$, an intuitive proof would be that we are changing the signs in the exponential tower, just like bits in binary numbers.
2. For non-periodic sequences, each $a(n)$ is unique, otherwise it would start to repeat.
3. Every $a(n)$ knows everything about every following $a(n)$, we can start on any $a(k)$ and generate all terms to $a(n)$.
4. $a(n)$ is not reversible, since we would loose track of the sign.

As a curiosity: to generate prime numbers out of “thin air” it would be enough to approximate one of the infinite $a_p(n)$, without explicit use of the prime sequence… (Yes, I had to naïvely run the first few $a_p(n)$ through oeis.org and the inverse symbolic calculator :))

Some questions

1. Have this method or constants similar to $a(0)$ been studied? (ie. any pointers to papers, terminology would be appreciated)

2. Could this method or constants have any meaningful mathematical value? (ie. maybe analytically looking at limits of segments, relations between different $a(0)$, zetas, Fourier stuff or whatever you math people do).

3. Would this method work for all primes? I guess this involves proving that $a(n)$ never can land exactly on 0, $\pm1$, $e^k$ or $\pm\Omega$ since log will then hit a singularity or get stuck. Or more generally which sequences would make $a(n)$ hit a singularity? I can only think of trivial cases.

4. Could it be beneficial to use complex numbers instead? (ie. can we remove the abs operation in the log chain? and maybe get some other improvements or insights? If we wanted to make $a(n)$ reversible how would one go about?)

If you have any thoughts on this feel free to contact me at jon AT jonkagstrom DOT com or twitter @jonkagstrom

Written with StackEdit.

Appendix

Plots of a(n) for a few sequences

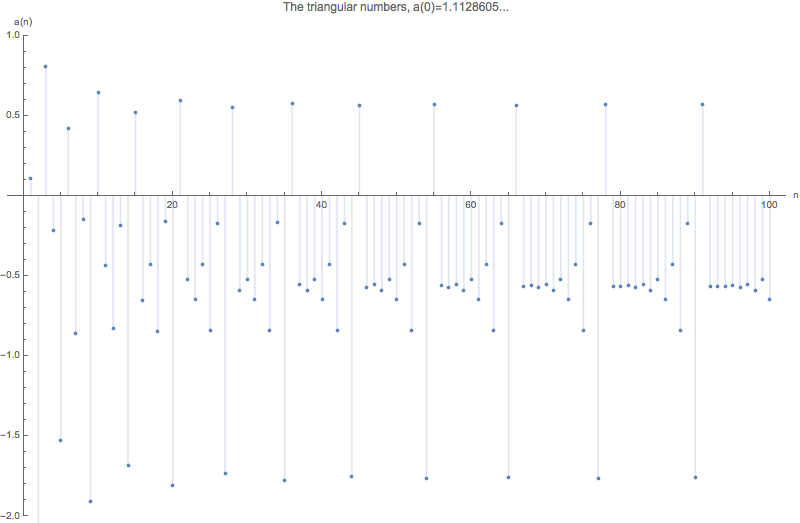
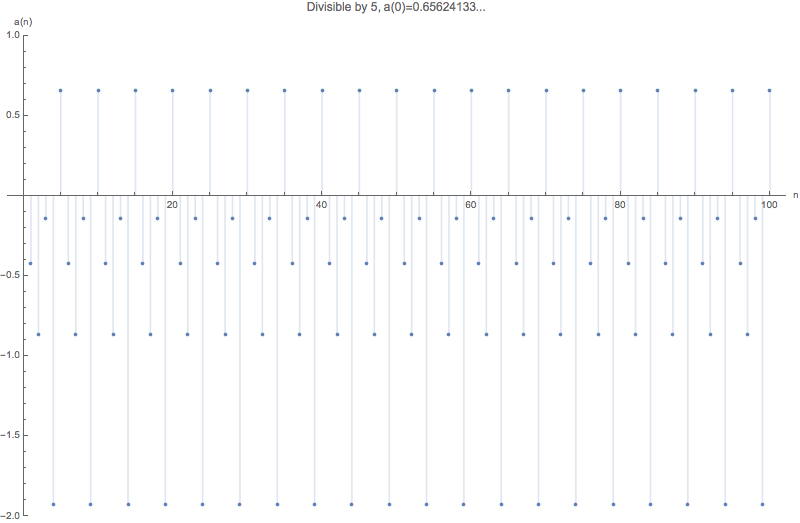
List of a(0) for a few sequences

Since the construction requires monotonicity, I took the partial sum variants of some of the sequences.

$a(0)$	Name	Oeis	Sequence
-0.02172268983561208427430192882333538885…	The prime numbers	A000040	2,3,5,7,11,13,17…
0.26987413757344922387738245114716164547…	Even numbers	A005843	0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,…
-0.74060688135103801777050535815859528166…	Lesser of twin primes	A001359	3, 5, 11, 17, 29, 41, 59, 71, 101
1.11286052331786308463253473339696820205…	The triangular numbers	A000217	0, 1, 3, 6, 10, 15, 21,…
1.23706976441655935195408275820389026770…	Partial sums of EKG sequence	A065057	0, 1, 3, 7, 13, 16, 25, 37, 45, 55,…
-1.30979958580415047766923370196817250601…	Odd numbers	A005408	1, 3, 5, 7, 9, 11, 13, 15, 17, 19,…
20.0489397450869111720804860862662653387…	Fibonacci numbers	A000045	0, 1, 1, 2, 3, 5, 8, 13, 21,…

First a(0)...a(20) for the primes

$n$	$a_p(n)$
0	-0.02172268983561208427430192882333538885
1	-3.8293979501655135483159747573148985010
2	1.34270759766814043682686741008233624606
3	0.29468817058065794491138757730797621956
4	-1.2218375305916203279064243952389325076
5	0.20035589822093328627173366934871756837
6	-1.6076600027479275838498989438858594072
7	0.47477970732279912092731661245732732516
8	-0.7449043565812110110542310619326298491
9	-0.2944994492719547241621216447774183101
10	-1.2224781459365405431384863141149501735
11	0.20088006567257572786592268763667428317
12	-1.6050472372084496901838231226540825152
13	0.47315318743141066082972698972332343369
14	-0.7483360794313098037606334197457176907
15	-0.2899030978619483118413203752247979295
16	-1.2382085571442250548849298473758673962
17	0.21366562303390746054560839474865456622
18	-1.5433429951381943601710094237143282883
19	0.43395083975915916099954231034904021916
20	-0.8348240237418737387497906595935156107

Stats for the first 1000 a(n) for the prime numberes

The separation between the bars represent the segmentation.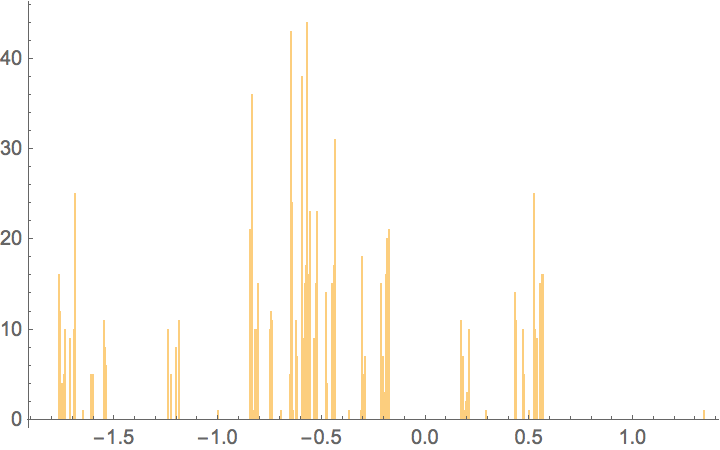

$sum=-547.5149136437048986805$
$mean=-0.547514913643704898680$
$median=-0.567133604277542465563$
$stddev= 0.627270814388245112504$

The first 256 decimals for a(0) for the prime numbers

-0.02172268983561208427430192882333538885414410223300617362296942014938449977851929711935503222059085888037984504484629308421587520474100857661240031214841994396285514186932586675876893907280886637173893965812055164688117774437897462730329816715911466784949783

This 256 digit $a_p(0)$ will produce the prime numbers correctly up to the prime number 1069 which is the 180th prime number.

First 4000 a(n) for the prime numbers

Mathematica code

The two important functions are the first two, sne(sf, n) and a(a0, n).

(* signed nested exponential (sne) calculates a0 for a sign function up to n terms *)
sne[sf_, n_] := (v = 0; For[i = n, i >= 0, i--, v = sf[i]*Exp[v]]; v);

(* calculates a(n) for n terms starting with a0 *)
a[a0_, n_] := (v = a0; For[i = 0, i < n, i++, v = Log[Abs[v]]]; v);

(* print a0 for a sign function *)
printA0[sf_, title_] := Print[title <> ", a(0)=" <> ToString[NumberForm[ N[sne[sf, 20]], 10]]];

(* plots each step of a(n) *)
plotAnFrom[a0_, n_, title_] :=
  DiscretePlot[a[a0, i], {i, 1, n}, 
   PlotLabel -> 
    title <> ", a(0)=" <> ToString[NumberForm[a0, 8]] <> "...",
   AxesLabel -> {"n", "a(n)"},
   ImageSize -> {800},
   Background -> Transparent,
   PlotRange -> {-2, 1}
   ];

(* First calculate a0 with some extra terms (to get better precision through out the plot), then plot it starting at a0 *)
plotAn[sf_, n_, title_] := (
   a0 = N[sne[sf, n + 10], n + 10]; 
   plotAnFrom[a0, n, title]
   );

(* some sign functions *)
oddSf[n_] := If[Mod[n, 2] != 0, 1, -1];
evenSf[n_] := If[Mod[n, 2] == 0, 1, -1];
mod5Sf[n_] := If[Mod[n, 5] == 0, 1, -1];
triangularSf[n_] := If[Mod[Sqrt[8*n + 1], 2] == 1, 1, -1];
primeSf[n_] := If[PrimeQ[n], 1, -1];

n = 100;
(* print a(0) *)
printA0[oddSf, "The odd numbers"];
printA0[evenSf, "The even numbers"];
printA0[mod5Sf, "Numbers divisible by 5"];
printA0[triangularSf, "The triangular numbers"];
printA0[primeSf, "The prime numbers"];

(* plot a(n) *)
plotAnFrom[3.0, n, "Example 1"]
plotAnFrom[2.0, n, "Example 2"]
plotAn[oddSf, n, "The odd numbers"]
plotAn[evenSf, n, "The even numbers"]
plotAn[mod5Sf, n, "Divisible by 5"]
plotAn[triangularSf, n, "The triangular numbers"]
plotAn[primeSf, n, "The prime numbers"]